Problem
Solving Strategy |
||
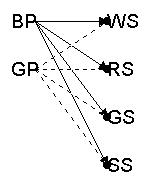
1. Doug has 2 pairs of pants: a black pair and a green pair. He has 4 shirts: a white shirt, a red shirt, a grey shirt and a striped shirt. How many different outfits can he put together?
| Draw a picture | Make a table | |||||||||||||||
 |
|
|||||||||||||||
| To check: | ||||||||||||||||
|
||||||||||||||||
| He can put 8 outfits together. | ||||||||||||||||
2. Ryan numbered his miniature race car collection according to the following rules:
a. It has to be a 3-digit number.
b. The digit in the hundreds place is less than 3.
c. The digit in the tens place is greater than 7.
d. The digit in the ones place is odd.
If Ryan used every possibility and each car had different number, how many cars did Ryan have in his collection?
Conditions |
|||||||||
| a. |
|
|
|
||||||
| b. |
|
<3 | |||||||
| 1, 2 | |||||||||
| c. |
|
>7 | |||||||
| 8, 9 | |||||||||
| d. |
|
odd | |||||||
| 1, 3, 5, 7, 9 | |||||||||
List systematically:
| begins with 18 |
begins with 19 |
begins with 28 |
begins with 29 |
| 181 | 191 | 281 | 291 |
| 183 | 193 | 283 | 293 |
| 185 | 195 | 285 | 295 |
| 187 | 197 | 287 | 297 |
| 189 | 199 | 289 | 299 |
| To check: | ||||||||
|
Ryan had 20 possibilities.
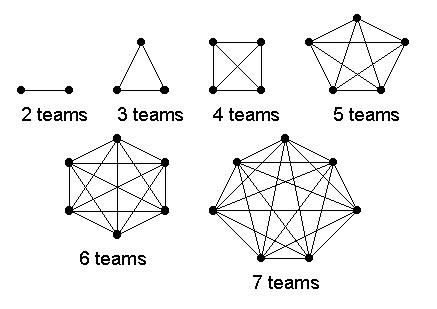
3. There will be 7 teams playing in the Maple Island Little League tournament. Each team is scheduled to play every other team once. How many games are scheduled for the tournament?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | No. | |
| 1 | / | / | / | / | / | / | 6 | |
| 2 | / | / | / | / | / | 5 | ||
| 3 | / | / | / | / | 4 | |||
| 4 | / | / | / | 3 | ||||
| 5 | / | / | 2 | |||||
| 6 | / | 1 | ||||||
| 7 | 0 | |||||||
| Total | 21 | |||||||
| To check: |
| (7 x 6) � 2 = 21 |
4. Marvin counted the marbles he had collected. He counted more than 40 but less than 70. When he put the marbles in groups of 5, he had 1 left over. When he put them in groups of 4, he had 1 left over. When he put them in groups of 3, he had 1 left over. How many marbles did Marvin collect?
To find the common number of marbles which can be put into groups of 3, 4 and 5 less the 1 left over is equivalent to finding the common multiple between 40 and 70.
| Begin with a multiple greater than 40. | ||||||||||
| 3: | ... | 42 | 45 | 48 | 51 | 54 | 57 | 60 | ||
| 4: | ... | 44 | 48 | 52 | 56 | 60 | ||||
| 5: | ... | 45 | 50 | 55 | 60 | |||||
OR simply 3 x 4 x 5 = 60
60 + 1 = 61 marbles
5. The number 475 is a three-digit number that uses only the three digits 4, 5, 7. How many three-digit numbers can be formed using these three digits, if repeated digits are allowed?
List systematically:
| 444 | 555 | 777 |
| 445 | 554 | 774 |
| 447 | 557 | 775 |
| 454 | 544 | 744 |
| 455 | 545 | 745 |
| 457 | 547 | 747 |
| 474 | 574 | 754 |
| 475 | 575 | 755 |
| 477 | 577 | 757 |
9 x 3 = 27 numbers
| To check: | ||||||||
|
6. I am a counting number. All three of my digits are odd but different. The sum of my digits is 13. The product of my digits is greater than 30. The sum of my tens’ and hundreds’ digits is less than my units’ digit. Which two numbers could I be?
Conditions |
|||||||||
| a. |
|
|
|
odd and different | |||||
| 1, 3, 5, 7, 9 | 1, 3, 5, 7, 9 | 1, 3, 5, 7, 9 | |||||||
| b. |
|
+ |
|
+ |
|
= 13 | |||
| 1, 3, 9 or 1, 6, 7 | |||||||||
| c. |
|
x |
|
x |
|
= 30 | |||
| 1, 5, 7 | |||||||||
| c. |
|
+ |
|
< |
|
157 and 517 | |||